RetroMagazine nr. 45 – Anno: 2023 – Autore: Eugenio Rapella
Le lettere che formano la “parola” EFBDCA sono le prime sei lettere dell’alfabeto. Qual è la parola, sempre formata da queste lettere, che le è immediatamente successiva in ordine alfabetico? Visto quanto richiesto, cercheremo, per quanto possibile, di mantenere inalterate le prime lettere per cui … partiremo dal fondo.
Le ultime due lettere sono CA; poiché C segue la A nell’ordine alfabetico, se le scambiassimo di posto, avremmo una parola (EFBDAC) precedente a quella in esame. Lo stesso vale per la coppia DC. Continuiamo a risalire esaminando le coppie di lettere contigue; ora è la volta di BD e questa volta, poiché B precede D avremo la possibilità di trovare una lettera a destra di B che ne potrà prendere il posto (al limite sarà la stessa D).
Naturalmente, se la parola di partenza fosse FEDCBA, non troveremmo la coppia adatta in quanto questa parola è l’ultima in ordine alfabetico formata dalle lettere considerate.
Con chi va scambiata la B? Tra tutte quelle a destra di B, ovvero DCA, sceglieremo quella che, in ordine alfabetico, la segue per prima. Siccome queste sono già disposte in ordine alfabetico inverso, basterà partire dall’ultima e risalire fino a trovare la prima che segue la nostra in ordine alfabetico. La A non va bene (A precede B), ma la C passa il test per cui scambieremo di posto la C e la B. Per ora abbiamo EFC seguito da DBA. Siamo agli sgoccioli: ci rimangono da sistemare le lettere dopo la C in modo che la “coda finale” sia … in ordine alfabetico. Lo scambio che abbiamo effettuato non ha variato l’ordine alfabetico di questa “coda” che risulta essere in ordine alfabetico inverso. Basterà semplicemente rovesciarla: DBA > ABD. Morale: l’anagramma di ABCDEF che segue EFBDCA nell’ordine alfabetico è EFCABD.
Il tutto ha l’aria un po’ complicata, ma è solo apparenza. Rivediamo i passaggi in modo più sintetico con un nuovo esempio: qual è l’anagramma di “CALZONI” che segue questa parola in ordine alfabetico? Usiamo il simbolo “<” per “precede” e “>” per “segue”. Abbiamo C>AO>N>I. Risalendo troviamo che la lettera da scambiare è la “L”. Tra le lettere a destra di L, qual è quella che la segue per prima? Loro sono già disposte in ordine decrescente, per cui, partendo dal fondo, I>L? No! N>L? Sì! Scambiamo L con N: CAN-ZOLI e ora invertiamo l’ordine delle ultime quattro lettere: CANILOZ. In ordine alfabetico, l’anagramma immediatamente seguente a CALZONI è CANILOZ.
Ecco come il nostro fidato C64 affronta e risolve il problema
100 input”scrivi una parola”;n$:d=len(n$):dim a(d)
110 for k=1 to d:a(k)=asc(mid$(n$,k,1)):next
120 print”premi un tasto per iniziare e”
130 print”per passare al successivo”
140 get r$: if r$=”” then 140
150 for k=1 to d:print chr$(a(k));:next:print
160 i=d-1
170 if a(i)>=a(i+1) then i=i-1:goto170
180 if i=0 then print:print “fine”:end
190 j=d
200 if a(j)<=a(i) then j=j-1:goto200
210 t=a(j):a(j)=a(i):a(i)=t
220 i=i+1:j=d
230 if i<j then t=a(j): a(j)=a(i): a(i)=t:i=i+1:j=j-1: goto 230
240 goto 140
I codici ASCII delle lettere che formano la parola, richiesta alla 100, vengono caricati nel vettore A(..); la dimensione di A(..) è D, pari alla lunghezza della parola (se N$=“amo”, è D=3 e A=(65,77,79)).
Alla 150 vengono stampate le lettere ora contenute in A(..); il programma vero e proprio inizia alla 160.
A partire dalla fine si confrontano le coppie di lettere contigue fino a trovare la prima coppia per cui A(I) precede A(I+1) (istr. 170): A(I) sarà la lettera da scambiare. Se l’anagramma è l’ultimo in ordine alfabetico, la variabile I raggiunge il valore 0 e il programma ha termine. Alle istruzioni 190-200 si riparte dal fondo alla ricerca della prima lettera A(J) che segue A(I): A(J) sarà la lettera da scambiare con A(I).
Alla 210 si esegue lo scambio e alla 220-230 si inverte l’ordine della coda; alla 240 si torna alla 140 per la stampa e per la ricerca dell’anagramma successivo.
Ecco un esempio di utilizzo:
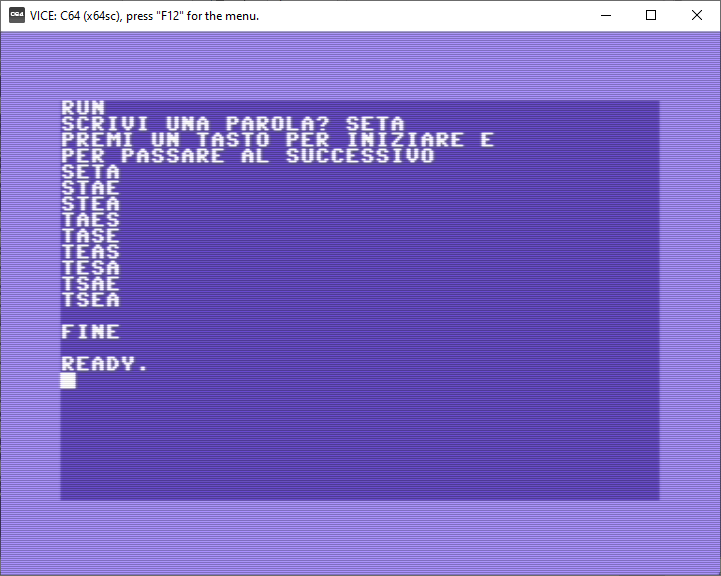
Ma … a cosa può servire un programma del genere? A non molto … però, se la parola iniziale è formata dalle prime N lettere in ordine alfabetico (ad esempio “abc” per N=3), il C64 ci fornisce tutti i possibili anagrammi, ovvero l’elenco delle permutazioni.
Abbandoniamo l’esempio letterale e riformuliamo il programma utilizzando i numeri da 1 a N. Ecco come:
100 input” n = “;n:dim a(n):f=1:c=0
110 for k=1 to n:a(k)=k:f=f*k:next
120 print”le permutazioni sono “;f
130 print”premi un tasto per iniziare e”
140 print”per passare alla perm successiva”
150 get r$: if r$=”” then 150
160 c=c+1
170 print:print” permutazione n: “;c
180 for k=1 to n:print a(k);:next:print
190 i=n-1
200 if a(i)>=a(i+1) then i=i-1:goto200
210 if i=0 then print:print “fine”:end
220 j=n
230 if a(j)<=a(i) then j=j-1:goto230
240 t=a(j):a(j)=a(i):a(i)=t
250 i=i+1:j=n
260 if i<j then t=a(j):a(j)=a(i):a(i)=t:i=i+1:j=j-1:goto 260
270 goto 150
Dopo aver richiesto N, il nostro C64 carica il vettore A(..) con i numeri da 1 a N e ne approfitta per calcolare il fattoriale di N (F=N!=1×2×3×..×N) che è il numero delle permutazioni che dovrà generare.
Il resto è identico al programma precedente, la variabile C funge da contatore delle varie permutazioni.
Ecco la schermata iniziale e quella finale di un esempio di utilizzo:
Naturalmente il codice può essere utilizzato come subroutine in programmi in cui è richiesto di generare tutte le permutazioni di N oggetti. Ecco allora un quesito che avevo proposto in una verifica per gli studenti del terzo anno di liceo:
Permutando in tutti i modi possibili le cifre 1,2,3,4,5 si ottengono 120 numeri naturali. Qual è la somma di questi 120 numeri?
Ovviamente agli studenti (e ai lettori di RMW) è richiesto di risolvere il problema con una … scorciatoia, ma il C64 può permettersi di eseguire la somma per esteso. Mettetevi al lavoro, confrontate poi la vostra soluzione con quella ottenuta dal programma qui sotto dove la permutazione contenuta nel vettore A(..) viene trasformata in numero nell’istruzione 130. Ogni cifra contribuisce alla creazione del numero V a seconda della sua posizione nel vettore A(..): A(1) “cifra delle unità”, A(2) “cifra delle decine” e così via. Quindi, se A=(2,5,1,4,3), avremo:
V=210^0+510^1+110^2+410^3+310^4= =2+50+100+4000+30000=34152
Alla 140 nella variabile S si aggiorna la somma dei vari valori per cui, alla fine, S contiene la soluzione.
100 n=5:dim a(n):c=0
110 for k=1 to n:a(k)=k:next
120 c=c+1:v=0
130 for k=1 to n:v=v+a(k)10^(k-1):next
140 print v;”addendo n.”;c:s=s+v
150 i=n-1
160 if a(i)>=a(i+1) then i=i-1:goto160
170 if i=0 then print:print”totale: “;s:end
180 j=n
190 if a(j)<=a(i) then j=j-1:goto190
200 t=a(j):a(j)=a(i):a(i)=t
210 i=i+1:j=n
220 if i<j then t=a(j):a(j)=a(i):a(i)=t:i=i+1:j=j-1:goto 220
230 goto 120
Direi che il nostro Commodore ha senz’altro superato la verifica, voi che ne dite?