Rivista: Commodore Professional – Numero: 1 – Anno 1987- Listato di: N/A
Francesco Sblendorio torna di nuovo protagonista di RetroLiPS con un altro listato per un computer a 16 bit, il Commodore Amiga.
Superfici 3D é un programma interamente scritto in AmigaBasic che permette di disegnare immagini tridimensionali sullo schermo del vostro Amiga e di cambiarne i colori a run-time.
Francesco aveva giá digitato il listato anni fa, ma é riuscito a recuperare informazioni relative alla rivista grazie a Stefano Benedetti che ha procurato le immagini delle pagine.
Il listato originale é stato pubblicato sulla rivista inglese Commodore Professional Numero 1di Agosto-Settembre 1987 – pag. 30.
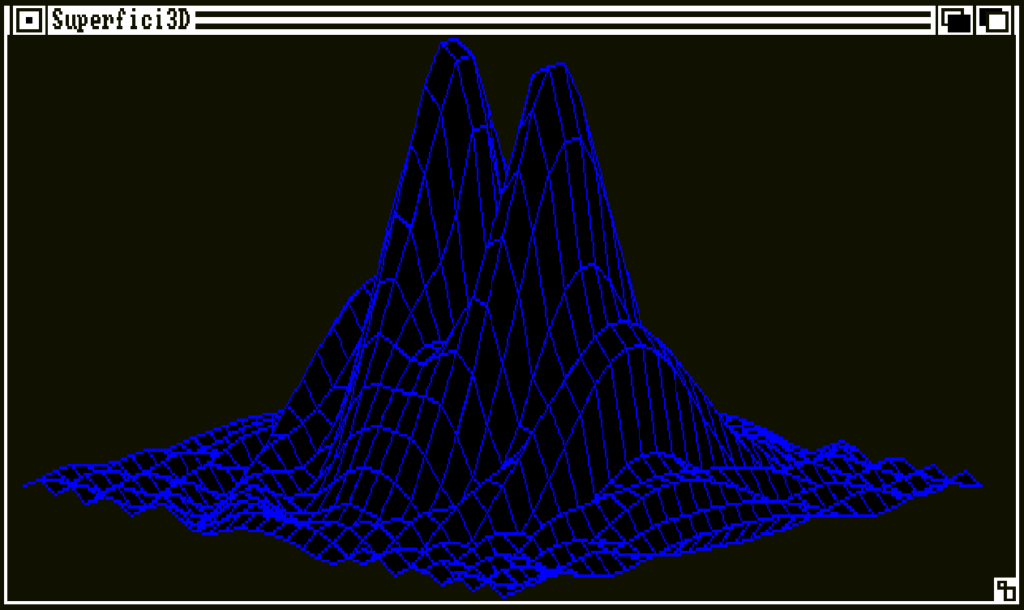
Titolo: Superfici 3D
Piattaforma: Commodore Amiga
Linguaggio: AmigaBASIC
Versione originale: N/A
Pubblicazione: Commodore Professional Nr. 1 – Agosto-Settembre 1987
Anno: 1987
Trascrizione: Francesco Sblendorio
Anno: 2022
Download: Superfici3D.zip contenente il file Superfici3D.ADF
Note: Il gioco funziona con l’AmigaBasic di Microsoft.
Istruzioni
Per cambiare il disegno del grafico, dovete modificare la formula FNz(x,y) definita nella procedura Equation:
DEF FNz(x,y)=SIN(x^2+3y^2)/(x^2+y^2)+(x^2+5y^2)EXP(1-x^2-y^2)/2
‘DEF FNz(x,y)=(x^2+5y^2)EXP(1-x^2-y^2)/2-SIN(3x^2+y^2)/(x^2+y^2)
‘DEF FNz(x,y)=(SIN(4x^2+y^2)+2SIN(x+y))/(4x^2+y^2)
‘DEF FNz(x,y)=SQR(ABS(xy))
Potete usare una delle 4 giá definite, oppure digitarne una nuova voi stessi. Buon divertimento!
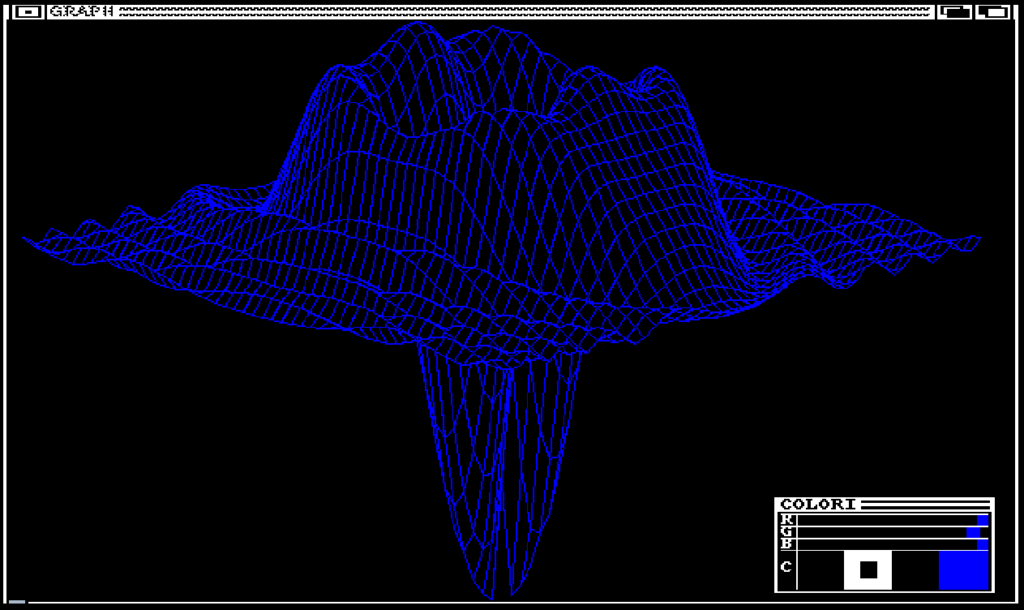
Oltre a modificare l’aspetto del grafico e i colori dello stesso, é possibile anche variare il dettaglio del disegno modificando i valori delle variabili m ed n. Queste sono settate di default a 31, prima immagine, ma settandole a 50, seconda immagine, il grafico risulterá molto piú definito. Non esagerate, oppure incorrerete in un errore di Out of Memory…
Qui di seguito trovate il codice ottimizzato per essere copiato su un file di testo ed essere scritto su un file ADF utilizzando il programma ADF Opus.
Se invece siete ansiosi di provare il programma su un Amiga reale o su un emulatore, suggerisco WinUAE, scaricate il file Superfici3D.zip contenente il file Superfici3D.ADF (creato da Francesco Sblendorio) e lanciate il file Superfici3D.bas.

PS – Se incontrate difficoltá ad utilizzare ADF Opus, WinUAE o l’AmigaBASIC, scriveteci: saremo lieti di aiutarvi!
Attenzione – Ci siamo resi conto che nel listato i caratteri ‘>’ e ‘<‘ potrebbero venir sostituiti dai rispettivi encoding html ‘>’ e ‘<’. Nel caso, sostituite questi valori nel listato prima di copiarlo sull’emulatore.
Listato: Superfici 3D – Commodore Amiga – AmigaBASIC
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
DEFINT i,j
pi=3.1415927# : e=2.7182818#
m=31 : n=31 ' dimensione del reticolo = m*n
res=1 ' risoluzione: 1=640*200, 2=640*400
gt=1 ' tipo di figura: 1=estimate 2=reale
asp=1 ' relazione x/y della figura (solitamente gt=1)
h=150 ' fattore di altezza (solamente per gt=1)
theta=30:phi=20 ' angoli d'osservazione in gradi (solamente per gt=2)
d=100 ' distanza dal centro della figura (solamente per gt=2)
lox=-3 : hix=3 ' limiti alto e basso nella direzione x
loy=-3 : hiy=3 ' limiti alto e basso nella direzione y
Equation:
DEF FNz(x,y)=SIN(x^2+3*y^2)/(x^2+y^2)+(x^2+5*y^2)*EXP(1-x^2-y^2)/2
'DEF FNz(x,y)=(x^2+5*y^2)*EXP(1-x^2-y^2)/2-SIN(3*x^2+y^2)/(x^2+y^2)
'DEF FNz(x,y)=(SIN(4*x^2+y^2)+2*SIN(x+y))/(4*x^2+y^2)
'DEF FNz(x,y)=SQR(ABS(x*y))
theta=theta*pi/180 : phi=phi*phi/180 ' conversione: gradi in radianti
a=d*COS(phi)*COS(theta)
b=d*COS(phi)*SIN(theta)
c=d*SIN(phi)
GOSUB Check
DIM xc(m+1,n+1),yc(m+1,n+1)
tx=(hix-lox)/m : ty=(hiy-loy)/n
CLS : PRINT : PRINT "Si stanno calcolando i valori..."
LOCATE 4,7 : PRINT m+1
IF gt=1 THEN GOSUB Estimate : ELSE GOSUB True
Draw:
IF res=2 THEN SCREEN 1,640,400,2,4 : WINDOW 2,"GRAPH",,14,1:ELSE CLS
DIM v(15),rgb(3,2) : p=0
Rc:
FOR c=0 TO 3
READ r,g,b
PALETTE c,r,g,b
rgb(c,0)=r : rgb(c,1)=g : rgb(c,2)=b
NEXT
DATA 0,0,0,.14,.14,.14,0,0,0,0,0,1
COLOR 2,3
FOR x=dfx TO dtx STEP sx
FOR y=dfy TO dty STEP sy
x1=xc(x,y) : x2=xc(x,y+1) : x3=xc(x+1,y+1) : x4=xc(x+1,y)
y1=yc(x,y) : y2=yc(x,y+1) : y3=yc(x+1,y+1) : y4=yc(x+1,y)
AREA (x1,y1) : AREA (x2,y2) : AREA (x3,y3) : AREA (x4,y4) : AREAFILL
LINE (x1,y1)-(x2,y2),3
LINE (x2,y2)-(x3,y3),3
LINE (x3,y3)-(x4,y4),3
LINE (x4,y4)-(x1,y1),3
NEXT
NEXT
Colors:
FOR n=0 TO 15
v(n)=11+7.54*n
NEXT
col=0 : x1=11 : x2=11 : x3=11
IF res=1 THEN WINDOW 3,"COLORI",(0,0)-(130,50),18,-1
IF res=2 THEN WINDOW 3,"COLORI",(0,0)-(130,50),18,1
WINDOW OUTPUT 3
PRINT "R" : PRINT "G" : PRINT "B" : PRINT : PRINT"C"
LINE (0,0)-(130,0) : LINE (0,8)-(130,8)
LINE (0,16)-(130,16) : LINE (0,24)-(130,24)
LINE (10,0)-(10,50) : LINE (11,25)-(40,50),0,BF
LINE (40,25)-(70,50),1,BF : LINE (70,25)-(100,50),2,BF
LINE (100,25)-(130,50),3,BF : LINE (11,1)-(19,7),3,BF
LINE (11,9)-(19,15),3,BF : LINE (11,17)-(19,23),3,BF
i=20 : LINE (20,32)-(30,42),1,BF
MENU 1,0,1,"Action" : MENU 1,1,1,"Quit"
MENU 2,0,0,"" : MENU 3,0,0,"" : MENU 4,0,0,""
MENU ON
Loop:
IF MENU(0)=1 AND MENU(1)=1 THEN
WINDOW CLOSE 3 : MENU RESET : WINDOW CLOSE 2 : SCREEN CLOSE 1 : STOP
END IF
x=MOUSE(1) : y=MOUSE(2) : IF MOUSE(0)>=0 THEN c1=1 : c2=1 : c3=1 : GOTO Loop
IF x>10 AND x<131 THEN IF y>24 AND y<51 THEN Getcol : ELSE GOTO Check1
GOTO Loop
Check1:
arg=.1260504*x-1.386551 : IF y<1 OR y>7 OR c1=0 THEN Check2
LINE (11,1)-(130,7),0,BF : LINE (v(arg),1)-(v(arg)+8,7),3,BF : x1=v(arg)
rgb(col,0)=arg/15 : PALETTE col,rgb(col,0),rgb(col,1),rgb(col,2)
c1=1 : c2=0 : c3=0 : GOTO Loop
Check2:
IF y<9 OR y>15 OR c2=0 THEN Check3
LINE (11,9)-(130,15),0,BF : LINE (v(arg),9)-(v(arg)+8,15),3,BF : x2=v(arg)
rgb(col,1)=arg/15 : PALETTE col,rgb(col,0),rgb(col,1),rgb(col,2)
c1=0 : c2=1 : c3=0 : GOTO Loop
Check3:
IF y<17 OR y>23 OR c3=0 THEN Loop
LINE (11,17)-(130,23),0,BF : LINE (v(arg),17)-(v(arg)+8,23),3,BF : x3=v(arg)
rgb(col,2)=arg/15 : PALETTE col,rgb(col,0),rgb(col,1),rgb(col,2)
c1=0 : c2=0 : c3=1 : GOTO Loop
Getcol:
LINE (i,32)-(i+10,42),col,BF
IF x<40 THEN i=20 : LINE (i,32)-(30,42),1,BF : col=0 : GOTO Nst
IF x<70 THEN i=50 : LINE (i,32)-(60,42),2,BF : col=1 : GOTO Nst
IF x<100 THEN i=80 : LINE (i,32)-(90,42),3,BF : col=2 : GOTO Nst
i=110 : LINE (i,32)-(120,42),0,BF : col=3
Nst:
LINE (11,1)-(130,23),0,BF : LINE (10,8)-(130,8) : LINE (10,16)-(130,16)
c=1
FOR n=0 TO 2 : t1=111*rgb(col,n)+11
LINE (t1,c)-(t1+8,c+6),3,BF : c=c+8
NEXT
GOTO Loop
Check:
m=INT(m) : n=INT(n)
asp=ABS(asp) : h=ABS(h)
IF res<>1 AND res<>2 THEN res=1
IF res=1 THEN ht=186 : hht=93
IF res=2 THEN ht=386 : hht=193
IF lox>hix THEN SWAP lox,hix
IF loy>hiy THEN SWAP loy,hiy
dfx=1 : dtx=m : sx=1 : dfy=1 : dty=n : sy=1
IF gt<>2 THEN gt=1
IF res<>2 THEN res=1
IF gt=2 THEN
IF a<0 THEN dfx=m : dtx=1 : sx=-1
IF b<0 THEN dfy=n : dty=1 : sy=-1
END IF
RETURN
Estimate:
m1=310/m : m2=160/m : n1=310/n : n2=160/n : rd=180/pi
x=240/SQR(1+asp^2) : y=240*asp/SQR(1+asp^2)
spx=310+.8886207*(x-y) : spy=hht-.4586429*(x+y)
x1=1.777241*x/m : x2=1.777241*y/n : y1=.9172858*x/m : y2=.9172858*y/n
i=0 : x=lox-tx
WHILE i<m+1
i=i+1 : LOCATE 5,7 : PRINT i;
x=x+tx : j=0 : y=loy-ty
WHILE j<n+1
j=j+1
y=y+ty
xc(i,j)=(spx+x2*j-x1*i)
yc(i,j)=spy+y2*j+y1*i-h*FNz(x,y)
IF yc(i,j)<smin THEN smin=yc(i,j)
IF yc(i,j)>smax THEN smax=yc(i,j)
WEND
WEND
IF smax<ht AND smin>0 THEN RETURN
avg=(smax+smin)/2 : smax=smax-avg : smin=smin-avg : mult=ht/(smax-smin)
FOR x=1 TO m+1
FOR y=1 TO n+1
yc(x,y)=mult*(yc(x,y)-avg)+hht
NEXT
NEXT
RETURN
True:
DEF FNc(a,b,c,x,y,z)=(x*(b*(b-y)+c*(c-z))+(x-a)*(b*y+c*z))/d
DEF FNang(x,y,z)=(px*x+py*y+pz*z)/(dp*SQR(x^2+y^2+z^2))
px=FNc(a,b,c,0,0,10)
py=FNc(b,a,c,0,0,10)
pz=FNc(c,b,a,10,0,0)
dp=SQR(px^2+py^2+pz^2)
i=0 : x=lox-tx
WHILE i<m+1
i=i+1 : LOCATE 5,7 : PRINT i
x=x+tx : j=0 : y=loy-ty
WHILE j<n+1
j=j+1
y=y+ty
xc(i,j)=FNz(x,y) : sum=sum+xc(i,j)
WEND
WEND
avg=sum/((m+1)*(n+1)) : ym=loy-ty-(loy+hiy)/2
i=0 : x=lox-tx-(lox+hix)/2
WHILE i<m+1
i=i+1 : LOCATE 6,7 : PRINT i
x=x+tx : j=0 : y=ym
WHILE j<n+1
j=j+1 : y=y+ty : z=xc(i,j)-avg
d=a*(a-x)+b*(b-y)+c*(c-z)
xc=FNc(a,b,c,x,y,z)
yc=FNc(b,a,c,y,x,z)
zc=FNc(c,b,a,z,y,x)
rad=SQR(xc^2+yc^2+zc^2)
s=1
IF SGN(a)<>SGN(yc*pz-zc*py) THEN
s=-1
ELSEIF SGN(b)<>SGN(zc*px-xc*pz) THEN
s=-1
ELSEIF SGN(c)<>SGN(xc*py-yc*px) THEN
s=-1
END IF
cs=FNang(xc,yc,zc) : sn=SQR(1.00001-cs^2)
xc(i,j)=s*rad*sn : yc(i,j)=-rad*cs
IF xc(i,j)>xmax THEN xmax=xc(i,j)
IF xc(i,j)<xmin THEN xmin=xc(i,j)
IF yc(i,j)>ymax THEN ymax=yc(i,j)
IF yc(i,j)<ymin THEN ymin=yc(i,j)
WEND
WEND
ax=(xmax+xmin)/2
ay=(ymax+ymin)/2
IF res=1 THEN
hzy=93
IF ((ymax-ymin)/(xmax-xmin))>(6.75/10.25) THEN
my=168/(ymax-ymin) : mx=168/(ymax-ymin)*2.200899
ELSE
my=602/(xmax-xmin)/2.200899 : mx=602/(xmax-xmin)
END IF
ELSE
hzy=193
IF ((ymax-ymin)/(xmax-xmin))>(6.875/10.25) THEN
my=368/(ymax-ymin) : mx=368/(ymax-ymin)*1.092089
ELSE
my=602/(xmax-xmin)/1.092089 : mx=602/(xmax-xmin)
END IF
END IF
FOR x=1 TO m+1
FOR y=1 TO n+1
xc(x,y)=315+mx*(xc(x,y)-ax)
yc(x,y)=hzy+my*(yc(x,y)-ay)
NEXT
NEXT
RETURN






One thought on “Superfici 3D – Amiga – AmigaBASIC”